|
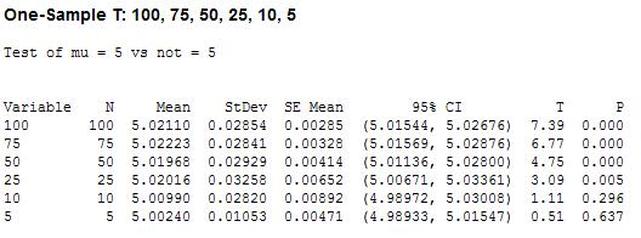
Hypothesis testing is an interesting subject. I can’t say that as a test engineer I use hypothesis testing on a regular basis, but it’s a useful thing to know a little bit about. The basic concept is that you have an idea of something being true (a hypothesis) and hypothesis testing coupled with a statistical method to analyze data is used in order to determine if your idea is true. For example, let’s say that under ideal conditions a voltage measurement will always measure 5 volts. Now, I want to know if I make the same measurement in a high humidity environment, will that significantly affect the measurement average. This becomes the null hypothesis and the alternate hypothesis. The null hypothesis is denoted by Ho and in this example is that the voltage measurement in high humidity is equal to 5 volts. The alternate hypothesis is denoted by H1 and is that the measurement under high humidity is not equal to 5 volts. It’s always confusing to me what is supposed to be the null hypothesis. The rule is that the null hypothesis is always assumed to be true. This is confusing because it depends on how you phase the null hypothesis, but here we are interested in a factor (humidity) altering the desired state of measuring 5 volts accurately. It doesn’t really matter what we think is going on. We might think that the humidity does have an effect, but until we can prove it (prove the alternate hypothesis is true) we assume the null hypothesis is true and everything is normal – 5 volts is measured accurately. I kind of think of it as the least interesting or default condition is always the null hypothesis. Example At this point it is easier to just turn the voltage measurement discussion above into an example. I used Labview to generate 100 random numbers to serve as the 5 volt measurements. I intentionally made the data skew slightly above 5 volts. I’m going to use the 1 sample T test in Minitab statistical software to perform the hypothesis testing. I should say that this is kind of trivial example, the real power is when you start using analysis of variance (ANOVA) to look at how multiple factors at multiple levels affect a process. The analysis was performed six times, each time reducing the number of samples that was used. Reducing the samples will illustrate how the decision to reject or fail to reject the null hypothesis becomes less certain. Figure 1 shows a partial screen shot of the data in Minitab. The columns are labeled with the number of samples in that column. Figure 1. Partial screen shot of measurement data of different sample sizes Figure 2 shows the output of the T test from Minitab. Figure 2. Results for 1 sample T test in Mintab of various sample sizes
In Figure 2 we can see that the column “N” is the number of samples. It shows that mean generally gets closer to 5 with fewer samples. The interesting result here is the P value in the last column. The results are not interpreted by the tool for us, but the rule is that since we are using a 95% confidence interval, any P value less than 0.05 would indicated that we should reject the null hypothesis. So, what’s all that mean? The P value is a probability value that tells us the probability that the null hypothesis is true. For N = 100, 75 and 50 it is saying that there is basically no possibility that the null hypothesis is true and we should reject the null hypothesis in favor of the alternate (and thus the humidity is having an effect). When N = 25 the P value is 0.005, which is still smaller than 0.05 and so we should still reject Ho. For N = 10 and 5 the sample size has gotten small enough that it’s now getting more likely that the mean is in fact 5 V, and we should fail to reject the null hypothesis. Figure 2 shows that we are using a default 95% confidence interval, that’s where the P value cut-off of 0.05 comes from (1 – 0.95 = 0.05). For N = 100, 75, 50 and 25 we are better than 95% confident that the mean is not 5V. You may be wondering why we would do all this. Why not just take a bunch of measurements and calculate the mean? That’s obviously important, but we can always argue that if we take way more measurements (samples) on top the current amount, then the mean will change. That’s why we use this tool, based on the number of samples, we can establish to with some level of confidence weather or not the mean is what we think it is. The results show that we get more and more confident as to the result as we add more samples. Hypothesis testing is also used by manufacturing and quality engineers where you have to sample a value from a process or a production line to try to figure out if the process is at the nominal value or drifting. Summary Hypothesis testing is a useful statistical concept for a test engineer to know and used by a lot of other technical people as well. This was a pretty simple explanation, but hopefully helpful. The steps in hypothesis testing are. 1. Determine your null hypothesis 2. Gather data 3. Assume the null hypothesis is true 4. Determine how much different you sampled values are different from your null hypothesis 5. Evaluate the P value P < 0.05 reject and P > 0.05 fail to reject. The mnemonic device is “If P is low, Ho must go”
2 Comments
Geethakakshmi PM
11/13/2022 08:26:19 pm
Thank you very much. I was wondering about the application of Null Hypothesis for technical subjects. Your article made me understand the necessity.
Reply
The article provides a clear explanation of the steps in hypothesis testing and how it is used by test engineers to determine if a hypothesis is true. The use of an example with varying sample sizes helps to illustrate how the decision to reject or fail to reject the null hypothesis becomes less certain. The article also provides an understanding of P values and how they are used to determine whether to reject or fail to reject the null hypothesis. Overall, it is a helpful article for those who want to learn more about hypothesis testing.
Reply
Your comment will be posted after it is approved.
Leave a Reply. |
Archives
December 2022
Categories
All
|
 RSS Feed
RSS Feed
