How Products Fail and Reliability

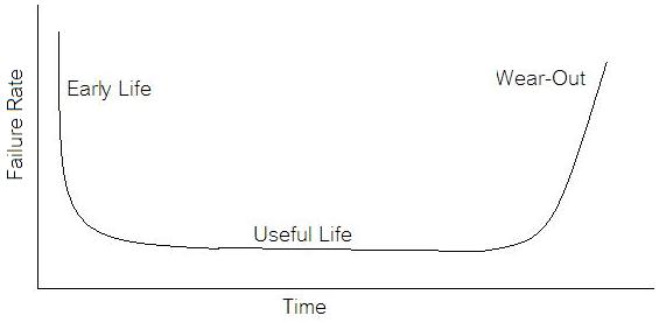
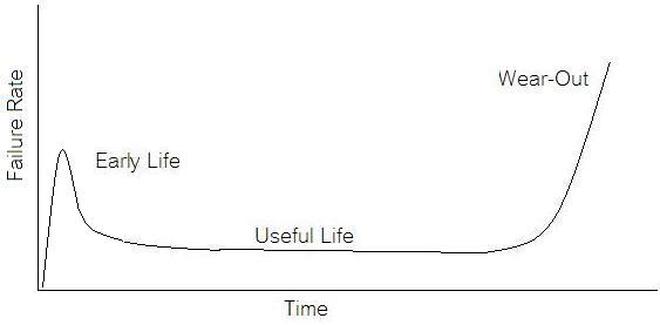
If we start talking about reliability instead of test engineering we are entering a whole different field of engineering. A test engineer is typically tasked with making sure a product is good when it goes out the door, the reliability engineer is concerned with trying to predict if a product will have a full useful life period. 

All electronics eventually fail if they are put to use. It may take a few minutes or decades. Since the job of a test engineer is to weed out the failures and defects it’s worthwhile for every test engineer to know a little bit about how products fail.

The Bathtub Curve

Reliability engineering involves heavy use of statistics and statistical distributions.  One of the most fundamental distributions of how products fail is the “bathtub curve.”

The idea of the bathtub curve, shown in Figure 1, is that a product goes through three general periods of failure rate. The three periods are, early life or infant mortality, the useful life period and the wear-out period. 

Figure 1. The Bathtub Curve

Figure 1 is pretty intuitive, in the early life period the failure rate is decreasing. This behavior is a result of weak products built with manufacturing defects that fail early. When all of those products have failed the failure rate is a constant low value for a long time until the product starts to wear out and the failure rate goes up again. Keep in mind that the curve is the average of a large population of the same product. The early life failure rate still might be very low, but it’s relatively higher than the useful life rate.

There is a lot more theory and thought behind the bathtub curve than I’m going to try to go over, because I’m not really concerned with that. There is also some controversy about whether the bathtub curve is realistic or not. The thinking seems to be that the curve could not start out with a decreasing failure rate in the early life period. Even if the early life failures occur very quickly, they did work for a short time and the failure rate should be going quickly up before decreasing (Figure 2). I can see this point, but I think regardless of the most accurate model, the concept of higher, lower, higher failure rates is valid. What I am concerned with is if we accept the idea that there are higher initial failure rates, what can test engineering do about it.

Figure 2. Modified Bathtub Curve: Increasing initial failure rate.

Accelerated Life Testing

Accelerated life testing or burn-in are general terms for testing that is designed to stress a product and reveal the early life failures before they can make it to the field. Some techniques include: high temperature operation, temperature cycling, humidity cycling, power cycling, elevated voltage level testing and vibration testing.

Burn-In

Burn-in, again, is a somewhat broad term. It might mean that a product will operate under normal conditions for some period of time or that it is operated under some set of severe conditions. The idea of operating the product under severe conditions, like high temperature, is to accelerate the process of finding early life failures. It may be the case that performing burn-in tests weakens good products as well as finding the faulty ones. This doesn’t mean that the whole thing is a waste, it can be helpful in determining the general failure rate of the product and the burn-in failures can be analyzed to determine what the underline defect was.

It is difficult to determine if it is worth-wile to setup a burn-in test step(s) when a product is manufactured. A big decision when using burn-in techniques is often when to stop. There has to be a trade off between finding the early life failure and just using up the useful life of good products. The cost of setting up a burn-in system should also be considered. Do you want to spend a lot of money and take a lot of time when burn-in just seems like a good idea? There is also a value lost in useful life and time that a product spends in burn-in during manufacturing.

To use burn-in you have to have some confidence that the product you are testing will have a higher early life failure rate settling to a low constant later. If the failure rate is just constant or worse always increasing with use of the product, then burn-in is just using up the life of the product and not doing any good to find the weak products.

Another criterion for burn-in is the useful life expectancy of the product. Semiconductors can last for decades, but over that time frame they will most likely be obsolete before they wear-out. In this case using up the useful life is not a big problem.

Personally, I’m somewhat skeptical of some types of burn-in tests. I think that burn-in is often done simply to give the feeling that everything possible has been done to find failures. If you are working in an industry where the products are hard to replace or man-critical then I can’t really argue too much. But if an occasional field failure is acceptable from time to time, burn-in should be considered more carefully.

I also have much more confidence in a burn-in test that performs some type of cycling where materials will be stressed by the changing environment. I’m skeptical of a test where a product is simply operated in constant conditions for some random period of time.

Extended Warranty

This isn’t exactly a test engineering matter, but knowing a little bit about how products fail gives us some insight into how warranties are used with consumer electronics. The manufacturers warranty usually covers the first 90 days or 1 year, which makes sense and is good, as this should cover the early life failures. However, retailers often want to sell you an extended warranty. Well, the bathtub curve would indicate that this is probably not going to pay off. I also have another way to think about it using a statistical concept called the expected value.

Informally, the expected value is what you can expect to happen given two events and two probabilities of those events occurring.

Here is the equation:

E(x) = x1p1 + x2p2

Where x1 and x2 are some events and p1 and p2 are the probabilities of those events occurring.  It’s often stated in the form of a game, like if we bet $5.00 with a 50% probability of winning $5.00 and a 50% probability of losing $5, then what is the average dollar amount we can expect to get? It would look like this:

-$5.00(0.5) + $5.00(0.5) = $0

The expected value is $0. Now, if we did this bet only one time we would either win or lose $5.00. However, the idea is to understand of the expected amount we would win or lose if it were possible to make this gamble a very large number of times.

It’s pretty simple to see how to evaluate a warranty using the expected value.

Let’s say you are going to buy a TV for $500 and the retailer wants to sell you an extended warranty for $100. We don’t know what the probability that the TV will fail will be, but it’s going to be pretty small. Keeping in mind that the larger portion of the failures (early life) will be covered by the manufacturer’s warranty, and then estimate it will fail 1% of the time.

The $500 dollars paid for the TV is gone either way. The game to evaluate with the expected value is paying $100 with a chance to “win” $400 (the cost of a $500 replacement TV minus the $100 warranty cost).

The expected value looks like this:

-$100(0.99) + $400(0.01) = -$95

Pretty good deal for the retailer. For the warranty to start paying off, the percentage of failing TVs has to go up to greater than 20%. It would be remarkably poor quality for a modern piece of consumer electronics to fail 20% of the time after the manufacturers warranty had expired.

Declining the warranty, you have automatically accepted the gamble that if the TV fails you will have to replace it at full cost. That would look like this (at 1% failure rate):

$0(0.99) + -$500(0.01) = -$5

Either gamble has a negative expected value, but relative to each other -$5 is a much better gamble than -$95.

Summary

The bathtub may not be a perfect model, but is a useful concept for a test engineer to be familiar with. Accelerated life testing and burn-in, when carefully considered, are an important test strategy tool for test engineering and insuring product reliability.